Klangfarbe Obertöne und Tonleiter:

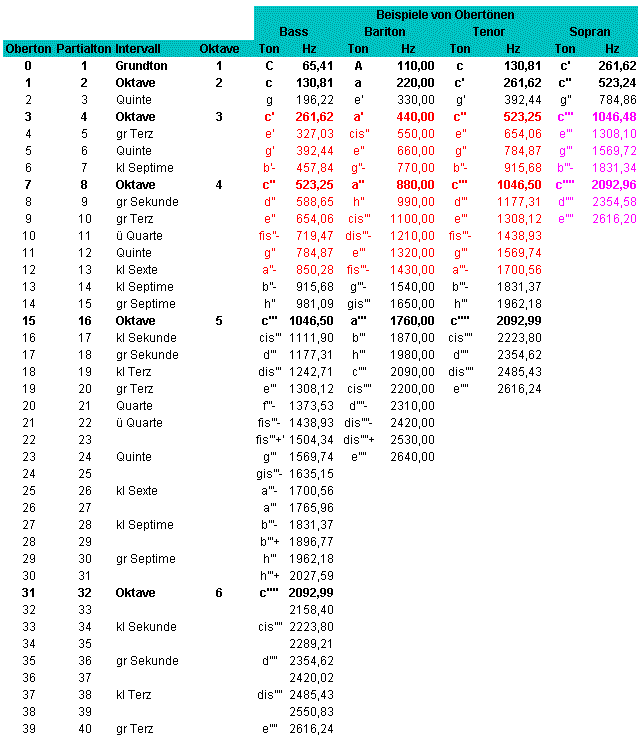
Ein elastischer Körper schwingt nicht nur in seiner Länge, sondern gleichzeitig auch in der Hälfte, dem Drittel, dem Viertel u.s.w. seiner Länge, und so erklingen mit dem Ton auch verschiedene andere Töne in unterschiedlicher Anzahl und Stärke mit.

Die meisten in der Musik verwendeter Töne bestehen aus einer Grundschwingung und mehreren, aber gewöhnlich auch schwächeren Obertönen. Unser Ohr nimmt aber diese Schwingungen nicht einzeln wahr, sondern vermischt alle zu einem Klang. Alle Oberschwingungen zusammen ergeben das, was wir mit unserem Ohr als Klangfarbe wahrnehmen. Vergleicht man den Klang eines Klaviers mit dem Klang einer Trompete, so wird man in der Obertonreihe ganz wesentliche Unterschiede feststellen; sowohl die Frequenzen als auch die Intensitäten der Obertöne der beiden Instrumente unterscheiden sich ganz wesentlich. Genau diese Differenz ist es, die die unterschiedlichen Klangfarben ausmachen. Töne ohne Oberschwingungen kommen in der Musik fast nie vor, weil fast alle Instrumente Töne mit Oberschwingungen, erzeugen. Töne ohne Oberschwingungen haben im zeitlichen Verlauf eine exakte Sinus. Mathematisch sind diese Zusammenhänge lange bekannt.

Kurzer Ausflug in die Welt der Technik

Wenn wir heute Musikaufnahmen machen werden verschiedene Verfahren verwendet. Analoge und Digitale Aufzeichnungsverfahren sind im Einsatz. Alle Verfahren können nicht die Realität (die direkte Wahrnehung) ersetzen auch wenn sie dieser sehr nahe kommen. Die Digitale Aufzeichnung verwendet die elektronische Speicherung und Rekonstruktion von Audiodaten, dabei hat sich ein Raster von 44100 Punkten pro Sekunde als Standard, etwa für CD´s etabliert. Bei der Wiedergabe werden die Lücken zwischen den Punkten glatt aufgefüllt. Vor allem für mehr oder weniger periodische Signalverläufe, hat jedoch die Frequenzdarstellung viele Vorteile. Sie ist auch als Fourierdarstellung bekannt, so benannt nach dem französischen Mathematiker, der ihre theoretischen Grundlagen erforscht hat. Die Basis ist folgende Bewandnis: ein vorgegebener Abschnitt eines zeitlichen Verlaufes, etwa des Schalldruckes, lässt sich als eine Summe von sinusförmigen Verläufen verstehen. Das heißt konkret: indem man mehrere Sinusfunktionen mit verschiedener Frequenz jeweils mit der richtigen Amplitude und Phasenlage zusammenaddiert, lässt sich jeder Verlauf der Kurve darstellen. Bezugnehmend auf die oben beschriebenen Darstellungen sind die benutzten sinusförmigen Funktionen die Basiselemente, die zu ihnen gehörigen Amplituden zusammen mit den Phasen die Koordinaten. Eine "Koordinate" ist also hier ein Paar von zwei Werten: Amplitude und Phase. Ein ausführlicher Artikel zum Problem der Darstellung von Tönen. Von Heinz Stolze, Institut für Stimme und Kommunikation, Bremen

Die Obertöne:

Die Obertöne oder Teiltöne, sind in der Tat die Reihenfolge der Obertöne, die nichts anderes sind als die unendliche Vervielfachung der Grundfrequenz (in Hz): 1f, 2f, 3f, 4f, 5f, 6f etc. ; Die Intervalle zwischen den Obertönen (1/2, 2/3, 3/4, 4/5, 5/6, 6/7, 7/8 usw.) bilden dann diejenigen Verhältnisse, deren arithmetische Abweichungen voneinander regelmäßig kleiner werden (1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7 usw.). Alle Intervallbestimmungen, und nicht temperiert sind, bezeichnet man als, mathematisch-rein oder als natürliche Harmonische Obertöne. Normalerweise wird davon ausgegangen, dass die Frequenzen der Obertöne ganzzahlige Vielfache der Frequenz des Grundtones sind. Solche Töne nennt man "harmonische" Töne. Das trifft bei den meisten Holzblasinstrumenten sehr gut zu, auch für viele Saiteninstrumente stimmt dies recht gut. Beim Klavier allerdings ist dieses ganzzahlige Frequenzverhältnis nur annähernd erfüllt. Besonders die sehr hohen Obertöne liegen schon recht weit neben den Frequenzen mit ganzzahligen Verhältnissen zum Grundton. Je höher wir die Leiter der Obertöne emporsteigen, desto mehr weichen deren Frequenzen von den genau harmonischen ab. Es hat sich sogar herausgestellt, dass die dem Klavier eigene Klangfarbe sehr wesentlich mit dieser Abweichung von den genau harmonischen Obertönen zusammenhängt. z.B. hören sich Imitationen eines Klaviers nicht besonders klavierähnlich an, wenn diese Abweichung der Obertonreihe bei der künstlichen Erzeugung des Tones nicht mit berücksichtigt wird. Das physikalische Gesetz, das der Teiltonreihe zugrunde liegt, findet auch beim praktischen Musizieren.

Anwendung:

Die Naturtonreihe, die Folge jener Töne welche ein Blechbläser nur durch Veränderung der Lippenspannung hervorbringen kann, entspricht einem Ausschnitt der Teiltonreihe.

Seit alter Zeit ist die Musiktheorie durch Anwendung und Erfahrung geprägt, also durch empirische und durch mathematisch rationale -Berechnungen. Von Pythagoras bis Euler, Keppler, Leibniz und Newton usw. es ist daher nichts neues sich mit Musiktheorie zu beschäftigen.

Die Klangfarbe eines Tones hängt von der Anzahl der mit dem Ton mitschwingenden Obertöne ab.

Die mit roten Pfeilen gekennzeichneten Teiltöne lassen sich im Notensystem nicht korrekt darstellen, da sie zu tief oder zu hoch sind (siehe Stimmung).

Aus den obenstehenden Zahlen lässt sich das Frequenzverhältnis der verschiedenen Intervalle ablesen, indem man immer die Intervalle nebeneinanderstehende Teiltöne nimmt.

z.B.: Zwischen dem 1. und dem 2. Teilton ist der Abstand eine Oktave, also hat eine Oktave die doppelte Frequenz des Ausgangstones (Verhältnis 1:2).

Die Intervalle, Zweiklänge, der natürliche Stimmung Ein Zweiklang wird von den meisten Musikhörern als schön empfunden, wenn sein Frequenzverhältnis nahe genug bei einem Verhältnis zweier nicht zu großer, natürlicher Zahlen m und n liegt. Die entsprechenden sog. Intervall haben Namen, zum Beispiel: Oktave für das Verhältnis 1:2. Entsprechend wird die Tonleiter bei der natürlichen Stimmung aufgebaut.

Halbton- und Ganztonschritte, gleichmäßige Stimmung

Die Einteilung der Dur Tonleiter entsteht durch Auswahl günstiger Tonfrequenzverhältnisse. Die Tonabstände sind innerhalb der natürlichen Tonleiter nicht immer gleich groß. So spricht man beim Übergang vom Mi nach Fa und von Ti nach Do von einem Halbtonschritt. Die anderen Übergänge (Do-Re, Re-Mi, Fa-So, So-La, La-Ti) sind Ganztonschritte. Somit besteht die Tonleiter aus 5 Ganztonschritten und 2 Halbtonschritten. Dies ergibt total 5 x 2 + 2 = 12 Halbtonschritte in einer Oktave. M n

Es ergeben sich aus der Teiltonreihe also folgende Frequenzverhältnisse:

Mit Hilfe dieser Frequenzverhältnisse kann man die Tonhöhe der einzelnen Teiltöne berechnen.

Rechenbeispiele:

1. Gesucht ist die Frequenz des e''.

Wie wir wissen, hat der Kammerton a' die Frequenz 440 Hz; das gesuchte e'' ist eine Quint höher als das a', das Frequenzverhältnis daher 2:3. Man dividiert nun die Frequenz des Ausgangstones mit 2 und multipliziert den erhaltenen Wert mit 3 und erhält so die gesuchte Frequenz des e''.

440 / 2 = 220 220 * 3 = 660 Hz e'' = 660 Hz. Um die Frequenz von e' zu erhalten transponiert man um eine Oktav nach unten. 660 / 2 = 330 Hz.

Neben der Oktav der Quint und der Terz bleibt als Intervall noch die Sekunde; diese hat schon Pythagoras als das Intervall zwischen der Quarte und der Quinte bestimmt, 2/3 - 3/4, also 2/3 x 4/3= 8/9. das Resultat ist im übrigen identisch mit 2/3 + 2/3 -1/2 (Quinte mit Oktavtransponierung), also 2/3 x 2/3 x 2/1 = 8/9. Die natürlich-harmonische Stimmung lautet also nun C D E F G . . c als Abfolge der Intervalle bezüglich des Grundtons: 1/1, 8/9, 4/5, 3/4, 2/3, 1/2. Alle restlichen Tonstufen werden bei der chromatischen Tonleiter aus den Intervallen 1:2,2:3.5:6 und deren Umkehrungen durch aneinander reihen aufgebaut.

Erwähnt sei noch, dass in letzter Zeit auch die Intervalle 6:7, 7:8 9:10 verwendet werden. Blues und Just Intonation zum Beispiel verwendet diese Intervalle.

Die chromatische Tonleiter:

In der chromatischen Tonleiter wird der Terz viel mehr Bedeutung zugemessen als zuvor. Erst im 12. Jahrhundert begann man, der Terz mehr Aufmerksamkeit zu schenken. Es wurde festgestellt, dass die Terzwerte der phythagoreischen Stimmung den kleineren Zahlenverhältnissen 5:6 für die kleine und 4:5 für die große Terz sehr nahe kamen. Später wurde dann zur Konstruktion der quint-terz-oktav-reinen Stimmung (auch: chromatische Stimmung) die Relationen 1:2 für die Oktave, 2:3 für die Quinte und 3:4 für die Quarte übernommen und zusätzlich die reine Terz mit 4:5 eingeführt.
Somit entspricht nun ein Schritt in Oktavrichtung der Multiplikation mit 1/2, ein Schritt in Quintrichtung der Multiplikation mit 2/3, einer in Terzrichtung der Multiplikation mit 4/5. Damit ergibt sich für einen Oktavausschnitt auf dem Grundton c_n folgende Tabelle:

Quint-terz-oktav-reine Stimmung heute:

Bei der Quint - Terz - Oktav reinen Stimmung werden Tönen, die im Sinne der Wohltemperierung gleich sind (wie cis und des, sowie dis und es oder auch gis und as) unterschiedliche Proportionen zugeordnet. Diese liegen jedoch sehr nahe beieinander, d.h. die Töne klingen ähnlich. Heutzutage ordnet man üblicherweise diesen Tönen die gleichen Proportionen zu, wie in der folgenden Tabelle gezeigt wird.

Reine Stimmung heute:

Die Tonleiter von ARISTOXENOS

Die Tonleiter von Giuseppe Zarlino (1517-90)

Wurde als Tonleiter der Physiker oder als natürliche Tonleiter bekannt.

Zarlinos Tonleiter mit allen Halbtönen.

Seite 146 musik-3.pdf Grundlagen der Musik

Quelle: http://www.riat-serra.org/akustik.html

Konstruktion der Tonleitern:

Werden fogende Intervalle voneinander abgezogen, ergeben sich folgende Ganz- und Halbtöne:

g-f =2/3 x 4/3 = 8/9 (großer Ganzton)

f-e =3/4 x 5/4 = 15/16 (Diatonischer Halbton)

e-d = 4/5 x 9/8 = 9/10 (kleiner Ganzton).

Auch reine Tonreihen haben also, sichtbar in der begrifflichen Unterscheidung ihrer Ganztöne,

Es ist der Abstand zwischen dem großen und dem kleinen Ganzton,

d-e = 8/9 x 10/9 = 80/81. Dieses syntonische oder diatonische Komma (Komma von Didymus) beträgt 21,506 Cent

Bei der hier erfolgten Konstruktion der natürlich-harmonischen Reihe fehlen noch die Töne des oberen Tetrachords a und h mit den Intervallen eines großen Ganztons, eines kleinen und eines Halbtones. Soll die Sexte möglichst rein klingen, wird zwischen g und a der kleine Ganzton platziert, 9/10, dann der große für H mit dem nachfolgenden Halbtonschritt, 15/16. Bezüglich des Grundtons bildet die Sexte den Bruch 3/5 als 2/3 x 9/10, die Septime 8/15 als 3/5 x 8/9 oder 1/2 x 16/15. Der Diatonischer Halbton.

Zum Aufbau der Toneiter werden vier Tonintervalle benutzt:

Die chromatische Tonleiter besteht aus einer Folge dieser drei Halbtonschritte:

Zum Aufbau des Tonstufen-Systems werden in der Folge des Quintenzirkels 3/2-Quinten benutzt, die Verminderungen der beiden Quinten d-a und b-f jeweils um ein syntonisches Komma (81/80 # 21.505 cent) werden durch Vergrößerung der fis – cis - Quinte um ein Diaschisma (2048/2025 # 19.550 cent) ausgeglichen:

Borduninstrumente benutzen Stimmungen, die bestimmte Harmonien mit dem Bordunton ergeben. Die Tabelle führt die gebräuchlichen Stimmungen auf:

Hier die Tabelle für die Highland Bagpipe. Die Quarte und die große Septime weichen von der "reinen" Stimmung ab.

Klassifizierung von Konsonanzgraden nach EULER

Im 18. Jahrhundert versuchte EULER die Konsonanz, den zentralen Begriff der Harmonielehre mathematisch auszudrücken. Als konsonant werden Intervalle bezeichnet, die als wohlklingend empfunden werden und nicht nach Auflösung in einen anderen Klang drängen; im Gegensatz hierzu werden Intervalle, die spannungsvoll empfunden werden, als dissonant bezeichnet. Als ein Kriterium für den Konsonanzgrad gilt die Einfachheit der Proportionen. Auf dieser Basis entwickelte EULER seine "gradus – suavitatis - Funktion", in die er Frequenzverhältnisse der reinen Stimmung einsetzte und somit den Konsonanzgrad von Frequenzproportionen mit ganzen, natürlichen Zahlen beschreiben konnte; je kleiner der Konsonanzgrad, desto wohlklingender ist das zugehörige Intervall. Es ergibt sich folgende Zuordnung von Frequenzproportionen zu Konsonanzgraden:

Beim Chor und Obertongesang werden ebenfalls die natürlichen Obertöne verwendet.

Um klarzustellen das bis jetzt Beschriebene ist nicht allgemeingültig es gibt verschiedene Intonationslagen!

Die wichtigsten Intonationslagen (Stimmungen) sind:

Reine Stimmung (Naturtonreihe) (16./17.Jh.)

Pythagoreische (Schichtung reiner Quinten) bis etwa 1450 n. Chr.

Mitteltönig temperiert (16./17. Jh.)

Wohltemperierte Stimmung (18.Jh.)

Werkmeister (Andreas) (sehr nahe der temperierten Intonation)

Kirnberger (ähnlich Werkmeister)

Gleichförmig temperierte Stimmung (Halbtonschritte =100 Cent)

Wie müssten bei der gleichförmig temperierten Stimmung diese 12 Halbtonschritte gewählt werden, damit die "Tonabstände" gleichmäßig sind? Gleichmäßige Abstände heißt, zwischen allen benachbarten Halbtönen muss das Frequenzverhältnis gleich sein. Um von einem Ton mit. Frequenz f auf die Frequenz des nächsthöheren Halbtons zu kommen muss man also f mit einem Faktor k multiplizieren. Dieser Faktor k soll bei allen Halbtönen in der Tonleiter der gleiche sein. Möchte man eine Oktave höher kommen, so durchläuft man alle 12 Halbtonschritte.: Bei "gleichem Tonabstand" muss der Quotient der Frequenzen benachbarter Halbtöne also 1.0594 betragen

In unserem Kulturkreis gilt seit ca. Ende 19. Jahrhundert die Meinung, dass die zwölftönig - gleichstufig, gleichförmig temperierte Stimmung anzuwenden ist. Die Abstände zwischen den 12 Halbtönen einer Oktave genau gleich. Heute gilt die verbreitete Meinung, dass die zwölftönig - gleichstufig temperierte Stimmung, die einharmonisch umgedeutet werden kann, anzuwenden ist. So ist heute diese Stimmung das meist angewendete System. Unsere elektronischen, für die Masse gedachter Stimmgeräte basieren auf dieser Technik. Besser sind Softwarestimmgeräte die mehrere Stimmungen unterstützen. Dementsprechend müssen wir uns zurechthören. Leicht zu Stimmende Intervalle sind: die Oktave, die Quint, die Quart. Die große Terz erlaubt einen größeren Spielraum, indem sie noch als "gestimmt" empfunden wird. Deshalb ist Intonation eine Auseinandersetzung mit reinen Quinten und reinen Terzen. Indiz für "Verstimmung" sind Schwebungen. langsame Schwebungen stören weniger, schnelle Schwebungen deuten auf "Verstimmtheit hin und werden unangenehm empfunden, sie reiben sich. Jeder Mensch hat seine eigenen Grenzen, wo er "Verstimmung" wahrnehmen kann. Angeblich hören im Bereich von c' ungefähr 50% von Konzertbesuchern einen Tonhöhenunterschied von 15 Cent, nur 24 % einen Tonhöhenunterschied von 7 Cent 10 % von Musizierenden hören noch einen Tonhöhenunterschied von 2 Cent, von den Nichtmusizierenden nur mehr 1 bis 2 %. Leider keine Quellenangabe zu diesen Daten.

Home | Kontakt | Sitemap | Impressum

© johann pascher